Python | How and where to apply Feature Scaling?

Feature Scaling or Standardization: It is a step of Data Pre Processing which is applied to independent variables or features of data. It basically helps to normalise the data within a particular range. Sometimes, it also helps in speeding up the calculations in an algorithm.

Package Used:

sklearn.preprocessing

Import:

 from sklearn.preprocessing import StandardScaler

Formula used in Backend
Standardisation replaces the values by their Z scores.

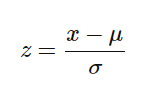
Mostly the Fit method is used for Feature scaling

fit(X, y = None)
Computes the mean and std to be used for later scaling.

import pandas as pd 
from sklearn.preprocessing import StandardScaler 
# Read Data from CSV 
data = read_csv('Geeksforgeeks.csv') 
data.head() 
# Initialise the Scaler 
scaler = StandardScaler() 
# To scale data 
scaler.fit(data) 

Why and Where to Apply Feature Scaling?
Real world dataset contains features that highly vary in magnitudes, units, and range. Normalisation should be performed when the scale of a feature is irrelevant or misleading and not should Normalise when the scale is meaningful.

The algorithms which use Euclidean Distance measure are sensitive to Magnitudes. Here feature scaling helps to weigh all the features equally.

Formally, If a feature in the dataset is big in scale compared to others then in algorithms where Euclidean distance is measured this big scaled feature becomes dominating and needs to be normalized.

Examples of Algorithms where Feature Scaling matters
1. K-Means uses the Euclidean distance measure here feature scaling matters.
2. K-Nearest-Neighbours also require feature scaling.
3. Principal Component Analysis (PCA): Tries to get the feature with maximum variance, here too feature scaling is required.
4. Gradient Descent: Calculation speed increase as Theta calculation becomes faster after feature scaling.

Note: Naive Bayes, Linear Discriminant Analysis, and Tree-Based models are not affected by feature scaling.
In Short, any Algorithm which is Not Distance based is Not affected by Feature Scaling.

ML | Feature Scaling – Part 1

Feature Scaling is a technique to standardize the independent features present in the data in a fixed range. It is performed during the data pre-processing.

Working:
Given a data-set with features- Age, Salary, BHK Apartment with the data size of 5000 people, each having these independent data features.
Each data point is labeled as:

Class1- YES (means with the given Age, Salary, BHK Apartment feature value one can buy the property)
Class2- NO (means with the given Age, Salary, BHK Apartment feature value one can’t buy the property).

Using dataset to train the model, one aims to build a model that can predict whether one can buy a property or not with given feature values.
Once the model is trained, an N-dimensional (where N is the no. of features present in the dataset) graph with data points from the given dataset, can be created. The figure given below is an ideal representation of the model.

As shown in the figure, star data points belong to Class1 – Yes and circles represent Class2 – No labels and the model gets trained using these data points. Now a new data point (diamond as shown in the figure) is given and it has different independent values for the 3 features (Age, Salary, BHK Apartment) mentioned above. The model has to predict whether this data point belongs to Yes or No.

Prediction of the class of new data point:
The model calculates the distance of this data point from the centroid of each class group. Finally this data point will belong to that class, which will have a minimum centroid distance from it.
The distance can be calculated between centroid and data point using these methods-

- Euclidean Distance : It is the square-root of the sum of squares of differences between the coordinates (feature values – Age, Salary, BHK Apartment) of data point and centroid of each class. This formula is given by Pythagorean theorem.
  where x is Data Point value, y is Centroid value and k is no. of feature values, Example: given data set has k = 3
- Manhattan Distance : It is calculated as the sum of absolute differences between the coordinates (feature values) of data point and centroid of each class.
- Minkowski Distance : It is a generalization of above two methods. As shown in the figure, different values can be used for finding r.

Need of Feature Scaling:
The given data set contains 3 features – Age, Salary, BHK Apartment. Consider a range of 10- 60 for Age, 1 Lac- 40 Lacs for Salary, 1- 5 for BHK of Flat. All these features are independent of each of other.
Suppose the centroid of class 1 is [40, 22 Lacs, 3] and data point to be predicted is [57, 33 Lacs, 2].
Using Manhattan Method,

Distance = (|(40 - 57)| + |(2200000 - 3300000)| + |(3 - 2)|)

It can be seen that Salary feature will dominate all other features while predicting the class of the given data point and since all the features are independent of each other i.e. a person’s salary has no relation with his/her age or what requirement of flat he/she has. This means that the model will always predict wrong.
So, the simple solution to this problem is Feature Scaling. Feature Scaling Algorithms will scale Age, Salary, BHK in fixed range say [-1, 1] or [0, 1]. And then no feature can dominate other.

ML | Feature Scaling – Part 2

Feature Scaling is a technique to standardize the independent features present in the data in a fixed range. It is performed during the data pre-processing to handle highly varying magnitudes or values or units. If feature scaling is not done, then a machine learning algorithm tends to weigh greater values, higher and consider smaller values as the lower values, regardless of the unit of the values.

Example: If an algorithm is not using feature scaling method then it can consider the value 3000 meter to be greater than 5 km but that’s actually not true and in this case, the algorithm will give wrong predictions. So, we use Feature Scaling to bring all values to same magnitudes and thus, tackle this issue.

Techniques to perform Feature Scaling
Consider the two most important ones:

Min-Max Normalization: This technique re-scales a feature or observation value with distribution value between 0 and 1.
Standardization: It is a very effective technique which re-scales a feature value so that it has distribution with 0 mean value and variance equals to 1.

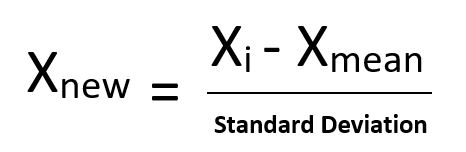
Download the dataset:
Go to the link and download Data_for_Feature_Scaling.csv

Below is the Python Code:

# Python code explaining How to 
# perform Feature Scaling 
  
""" PART 1 
    Importing Libraries """
  
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 
 
# Sklearn library  
from sklearn import preprocessing 
 
""" PART 2 
    Importing Data """
  
data_set = pd.read_csv('C:\\Users\\dell\\Desktop\\Data_for_Feature_Scaling.csv') 
data_set.head() 
 
# here Features - Age and Salary columns  
# are taken using slicing 
# to handle values with varying magnitude 
x = data_set.iloc[:, 1:3].values 
print ("\nOriginal data values : \n",  x) 
 
 
""" PART 4 
    Handling the missing values """
 
from sklearn import preprocessing 
 
""" MIN MAX SCALER """
 
min_max_scaler = preprocessing.MinMaxScaler(feature_range =(0, 1)) 
 
# Scaled feature 
x_after_min_max_scaler = min_max_scaler.fit_transform(x) 
 
print ("\nAfter min max Scaling : \n", x_after_min_max_scaler) 
 
 
""" Standardisation """
 
Standardisation = preprocessing.StandardScaler() 
 
# Scaled feature 
x_after_Standardisation = Standardisation.fit_transform(x) 
 
print ("\nAfter Standardisation : \n", x_after_Standardisation) 

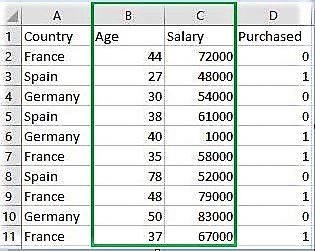
Output :

   Country  Age  Salary  Purchased
0   France   44   72000          0
1    Spain   27   48000          1
2  Germany   30   54000          0
3    Spain   38   61000          0
4  Germany   40    1000          1

Original data values : 
 [[   44 72000]
 [   27 48000]
 [   30 54000]
 [   38 61000]
 [   40  1000]
 [   35 58000]
 [   78 52000]
 [   48 79000]
 [   50 83000]
 [   37 67000]]

After min max Scaling : 
 [[ 0.33333333  0.86585366]
 [ 0.          0.57317073]
 [ 0.05882353  0.64634146]
 [ 0.21568627  0.73170732]
 [ 0.25490196  0.        ]
 [ 0.15686275  0.69512195]
 [ 1.          0.62195122]
 [ 0.41176471  0.95121951]
 [ 0.45098039  1.        ]
 [ 0.19607843  0.80487805]]

After Standardisation : 
 [[ 0.09536935  0.66527061]
 [-1.15176827 -0.43586695]
 [-0.93168516 -0.16058256]
 [-0.34479687  0.16058256]
 [-0.1980748  -2.59226136]
 [-0.56487998  0.02294037]
 [ 2.58964459 -0.25234403]
 [ 0.38881349  0.98643574]
 [ 0.53553557  1.16995867]
 [-0.41815791  0.43586695]]