K-Nearest Neighbours
K-Nearest Neighbors is one of the most basic yet essential classification algorithms in Machine Learning. It belongs to the supervised learning domain and finds intense application in pattern recognition, data mining and intrusion detection.
It is widely disposable in real-life scenarios since it is non-parametric, meaning, it does not make any underlying assumptions about the distribution of data (as opposed to other algorithms such as GMM, which assume a Gaussian distribution of the given data).
We are given some prior data (also called training data), which classifies coordinates into groups identified by an attribute.
As an example, consider the following table of data points containing two features:

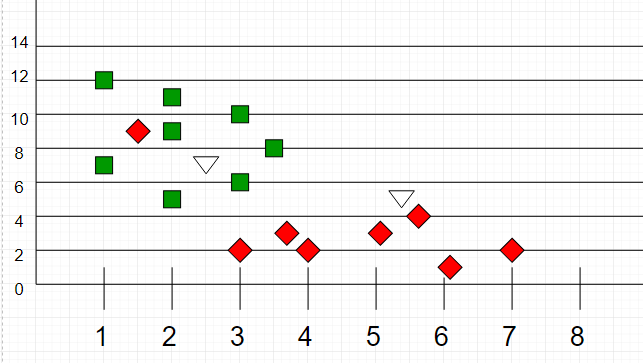
Now, given another set of data points (also called testing data), allocate these points a group by analyzing the training set. Note that the unclassified points are marked as ‘White’.
Intuition
If we plot these points on a graph, we may be able to locate some clusters or groups. Now, given an unclassified point, we can assign it to a group by observing what group its nearest neighbors belong to. This means a point close to a cluster of points classified as ‘Red’ has a higher probability of getting classified as ‘Red’.
Intuitively, we can see that the first point (2.5, 7) should be classified as ‘Green’ and the second point (5.5, 4.5) should be classified as ‘Red’.
Algorithm
Let m be the number of training data samples. Let p be an unknown point.
- Store the training samples in an array of data points arr[]. This means each element of this array represents a tuple (x, y).
-
for i=0 to m: Calculate Euclidean distance d(arr[i], p).
- Make set S of K smallest distances obtained. Each of these distances corresponds to an already classified data point.
- Return the majority label among S.
K can be kept as an odd number so that we can calculate a clear majority in the case where only two groups are possible (e.g. Red/Blue). With increasing K, we get smoother, more defined boundaries across different classifications. Also, the accuracy of the above classifier increases as we increase the number of data points in the training set.
Example Program
Assume 0 and 1 as the two classifiers (groups).
- C/C++
- Python
play_arrow
brightness_4
// C++ program to find groups of unknown // Points using K nearest neighbour algorithm. #include <bits/stdc++.h> using namespace std; struct Point { int val; // Group of point double x, y; // Co-ordinate of point double distance; // Distance from test point }; // Used to sort an array of points by increasing // order of distance bool comparison(Point a, Point b) { return (a.distance < b.distance); } // This function finds classification of point p using // k nearest neighbour algorithm. It assumes only two // groups and returns 0 if p belongs to group 0, else // 1 (belongs to group 1). int classifyAPoint(Point arr[], int n, int k, Point p) { // Fill distances of all points from p for (int i = 0; i < n; i++) arr[i].distance = sqrt((arr[i].x - p.x) * (arr[i].x - p.x) + (arr[i].y - p.y) * (arr[i].y - p.y)); // Sort the Points by distance from p sort(arr, arr+n, comparison); // Now consider the first k elements and only // two groups int freq1 = 0; // Frequency of group 0 int freq2 = 0; // Frequency of group 1 for (int i = 0; i < k; i++) { if (arr[i].val == 0) freq1++; else if (arr[i].val == 1) freq2++; } return (freq1 > freq2 ? 0 : 1); } // Driver code int main() { int n = 17; // Number of data points Point arr[n]; arr[0].x = 1; arr[0].y = 12; arr[0].val = 0; arr[1].x = 2; arr[1].y = 5; arr[1].val = 0; arr[2].x = 5; arr[2].y = 3; arr[2].val = 1; arr[3].x = 3; arr[3].y = 2; arr[3].val = 1; arr[4].x = 3; arr[4].y = 6; arr[4].val = 0; arr[5].x = 1.5; arr[5].y = 9; arr[5].val = 1; arr[6].x = 7; arr[6].y = 2; arr[6].val = 1; arr[7].x = 6; arr[7].y = 1; arr[7].val = 1; arr[8].x = 3.8; arr[8].y = 3; arr[8].val = 1; arr[9].x = 3; arr[9].y = 10; arr[9].val = 0; arr[10].x = 5.6; arr[10].y = 4; arr[10].val = 1; arr[11].x = 4; arr[11].y = 2; arr[11].val = 1; arr[12].x = 3.5; arr[12].y = 8; arr[12].val = 0; arr[13].x = 2; arr[13].y = 11; arr[13].val = 0; arr[14].x = 2; arr[14].y = 5; arr[14].val = 1; arr[15].x = 2; arr[15].y = 9; arr[15].val = 0; arr[16].x = 1; arr[16].y = 7; arr[16].val = 0; /*Testing Point*/ Point p; p.x = 2.5; p.y = 7; // Parameter to decide group of the testing point int k = 3; printf ("The value classified to unknown point" " is %d.\n", classifyAPoint(arr, n, k, p)); return 0; } |
Output:
The value classified to unknown point is 0.
Implementation of K Nearest Neighbors
Prerequisite : K nearest neighbours
Introduction
Say we are given a data set of items, each having numerically valued features (like Height, Weight, Age, etc). If the count of features is n, we can represent the items as points in an n-dimensional grid. Given a new item, we can calculate the distance from the item to every other item in the set. We pick the k closest neighbors and we see where most of these neighbors are classified in. We classify the new item there.
So the problem becomes how we can calculate the distances between items. The solution to this depends on the data set. If the values are real we usually use the Euclidean distance. If the values are categorical or binary, we usually use the Hamming distance.
Algorithm:
Given a new item:
1. Find distances between new item and all other items
2. Pick k shorter distances
3. Pick the most common class in these k distances
4. That class is where we will classify the new item
Reading Data
Let our input file be in the following format:
Height, Weight, Age, Class 1.70, 65, 20, Programmer 1.90, 85, 33, Builder 1.78, 76, 31, Builder 1.73, 74, 24, Programmer 1.81, 75, 35, Builder 1.73, 70, 75, Scientist 1.80, 71, 63, Scientist 1.75, 69, 25, Programmer
Each item is a line and under “Class” we see where the item is classified in. The values under the feature names (“Height” etc.) is the value the item has for that feature. All the values and features are separated by commas.
Place these data files in the working directory data2 and data. Choose one and paste the contents as is into a text file named data.
We will read from the file (named “data.txt”) and we will split the input by lines:
f = open('data.txt', 'r');
lines = f.read().splitlines();
f.close();
The first line of the file holds the feature names, with the keyword “Class” at the end. We want to store the feature names into a list:
# Split the first line by commas,
# remove the first element and
# save the rest into a list. The
# list now holds the feature
# names of the data set.
features = lines[0].split(', ')[:-1];
Then we move onto the data set itself. We will save the items into a list, named items, whose elements are dictionaries (one for each item). The keys to these item-dictionaries are the feature names, plus “Class” to hold the item class. At the end, we want to shuffle the items in the list (this is a safety measure, in case the items are in a weird order).
items = []; for i in range(1, len(lines)): line = lines[i].split(', '); itemFeatures = {"Class" : line[-1]}; # Iterate through the features for j in range(len(features)): # Get the feature at index j f = features[j]; # The first item in the line # is the class, skip it v = float(line[j]); # Add feature to dict itemFeatures[f] = v; # Append temp dict to items items.append(itemFeatures); shuffle(items); |
Classifying the data
With the data stored into items, we now start building our classifier. For the classifier, we will create a new function, Classify. It will take as input the item we want to classify, the items list and k, the number of the closest neighbors.
If k is greater than the length of the data set, we do not go ahead with the classifying, as we cannot have more closest neighbors than the total amount of items in the data set. (alternatively we could set k as the items length instead of returning an error message)
if(k > len(Items)):
# k is larger than list
# length, abort
return "k larger than list length";
We want to calculate the distance between the item to be classified and all the items in the training set, in the end keeping the k shortest distances. To keep the current closest neighbors we use a list, called neighbors. Each element in the least holds two values, one for the distance from the item to be classified and another for the class the neighbor is in. We will calculate distance via the generalized Euclidean formula (for n dimensions). Then, we will pick the class that appears most of the time in neighbors and that will be our pick. In code:
def Classify(nItem, k, Items): if(k > len(Items)): # k is larger than list # length, abort return "k larger than list length"; # Hold nearest neighbors. # First item is distance, # second class neighbors = []; for item in Items: # Find Euclidean Distance distance = EuclideanDistance(nItem, item); # Update neighbors, either adding # the current item in neighbors # or not. neighbors = UpdateNeighbors(neighbors, item, distance, k); # Count the number of each # class in neighbors count = CalculateNeighborsClass(neighbors, k); # Find the max in count, aka the # class with the most appearances. return FindMax(count); |
The external functions we need to implement are EuclideanDistance, UpdateNeighbors, CalculateNeighborsClass and FindMax.
Finding Euclidean Distance
The generalized Euclidean formula for two vectors x and y is this:
distance = sqrt{(x_{1}-y_{1})^2 + (x_{2}-y_{2})^2 + ... + (x_{n}-y_{n})^2}
In code:
def EuclideanDistance(x, y): # The sum of the squared # differences of the elements S = 0; for key in x.keys(): S += math.pow(x[key]-y[key], 2); # The square root of the sum return math.sqrt(S); |
Updating Neighbors
We have our neighbors list (which should at most have a length of k) and we want to add an item to the list with a given distance. First we will check if neighbors has a length of k. If it has less, we add the item to it irregardless of the distance (as we need to fill the list up to k before we start rejecting items). If not, we will check if the item has a shorter distance than the item with the max distance in the list. If that is true, we will replace the item with max distance with the new item.
To find the max distance item more quickly, we will keep the list sorted in ascending order. So, the last item in the list will have the max distance. We will replace it with the new item and we will sort again.
To speed this process up, we can implement an Insertion Sort where we insert new items in the list without having to sort the entire list. The code for this though is rather long and, although simple, will bog the tutorial down.
def UpdateNeighbors(neighbors, item, distance, k): if(len(neighbors) > distance): # If yes, replace the last # element with new item neighbors[-1] = [distance, item["Class"]]; neighbors = sorted(neighbors); return neighbors; |
CalculateNeighborsClass
Here we will calculate the class that appears most often in neighbors. For that, we will use another dictionary, called count, where the keys are the class names appearing in neighbors. If a key doesn’t exist, we will add it, otherwise we will increment its value.
def CalculateNeighborsClass(neighbors, k): count = {}; for i in range(k): if(neighbors[i][1] not in count): # The class at the ith index # is not in the count dict. # Initialize it to 1. count[neighbors[i][1]] = 1; else: # Found another item of class # c[i]. Increment its counter. count[neighbors[i][1]] += 1; return count; |
FindMax
We will input to this function the dictionary count we build in CalculateNeighborsClass and we will return its max.
def FindMax(countList): # Hold the max maximum = -1; # Hold the classification classification = ""; for key in countList.keys(): if(countList[key] > maximum): maximum = countList[key]; classification = key; return classification, maximum; |
Conclusion
With that this kNN tutorial is finished.
You can now classify new items, setting k as you see fit. Usually for k an odd number is used, but that is not necessary. To classify a new item, you need to create a dictionary with keys the feature names and the values that characterize the item. An example of classification:
newItem = {'Height' : 1.74, 'Weight' : 67, 'Age' : 22};
print Classify(newItem, 3, items);
The complete code of the above approach is given below:-
play_arrow
brightness_4
# Python Program to illustrate # KNN algorithm # For pow and sqrt import math from random import shuffle ###_Reading_### def ReadData(fileName): # Read the file, splitting by lines f = open(fileName, 'r') lines = f.read().splitlines() f.close() # Split the first line by commas, # remove the first element and save # the rest into a list. The list # holds the feature names of the # data set. features = lines[0].split(', ')[:-1] items = [] for i in range(1, len(lines)): line = lines[i].split(', ') itemFeatures = {'Class': line[-1]} for j in range(len(features)): # Get the feature at index j f = features[j] # Convert feature value to float v = float(line[j]) # Add feature value to dict itemFeatures[f] = v items.append(itemFeatures) shuffle(items) return items ###_Auxiliary Function_### def EuclideanDistance(x, y): # The sum of the squared differences # of the elements S = 0 for key in x.keys(): S += math.pow(x[key] - y[key], 2) # The square root of the sum return math.sqrt(S) def CalculateNeighborsClass(neighbors, k): count = {} for i in range(k): if neighbors[i][1] not in count: # The class at the ith index is # not in the count dict. # Initialize it to 1. count[neighbors[i][1]] = 1 else: # Found another item of class # c[i]. Increment its counter. count[neighbors[i][1]] += 1 return count def FindMax(Dict): # Find max in dictionary, return # max value and max index maximum = -1 classification = '' for key in Dict.keys(): if Dict[key] > maximum: maximum = Dict[key] classification = key return (classification, maximum) ###_Core Functions_### def Classify(nItem, k, Items): # Hold nearest neighbours. First item # is distance, second class neighbors = [] for item in Items: # Find Euclidean Distance distance = EuclideanDistance(nItem, item) # Update neighbors, either adding the # current item in neighbors or not. neighbors = UpdateNeighbors(neighbors, item, distance, k) # Count the number of each class # in neighbors count = CalculateNeighborsClass(neighbors, k) # Find the max in count, aka the # class with the most appearances return FindMax(count) def UpdateNeighbors(neighbors, item, distance, k, ): if len(neighbors) < k: # List is not full, add # new item and sort neighbors.append([distance, item['Class']]) neighbors = sorted(neighbors) else: # List is full Check if new # item should be entered if neighbors[-1][0] > distance: # If yes, replace the # last element with new item neighbors[-1] = [distance, item['Class']] neighbors = sorted(neighbors) return neighbors ###_Evaluation Functions_### def K_FoldValidation(K, k, Items): if K > len(Items): return -1 # The number of correct classifications correct = 0 # The total number of classifications total = len(Items) * (K - 1) # The length of a fold l = int(len(Items) / K) for i in range(K): # Split data into training set # and test set trainingSet = Items[i * l:(i + 1) * l] testSet = Items[:i * l] + Items[(i + 1) * l:] for item in testSet: itemClass = item['Class'] itemFeatures = {} # Get feature values for key in item: if key != 'Class': # If key isn't "Class", add # it to itemFeatures itemFeatures[key] = item[key] # Categorize item based on # its feature values guess = Classify(itemFeatures, k, trainingSet)[0] if guess == itemClass: # Guessed correctly correct += 1 accuracy = correct / float(total) return accuracy def Evaluate(K, k, items, iterations): # Run algorithm the number of # iterations, pick average accuracy = 0 for i in range(iterations): shuffle(items) accuracy += K_FoldValidation(K, k, items) print accuracy / float(iterations) ###_Main_### def main(): items = ReadData('data.txt') Evaluate(5, 5, items, 100) if __name__ == '__main__': main() |
Output:
0.9375
The output can vary from machine to machine. The code includes a Fold Validation function, but it is unrelated to the algorithm, it is there for calculating the accuracy of the algorithm.
