Data Structures and Algorithms for Interviews

Demo Video

 

Demo video1:   Delete a node in BST

Demo video2:   Delete first node in CLL

Data Structures and Algorithms

Data Structures for interviews course at Algorithm Training training institute requires prior knowledge from students on Data Structures and Algorithms. This training targets top MNC interviews. This Training would be very useful for in and off campus placements for students from IITs, NITs, BITs, IIITs, Universities and other top engineering students. Here we are going to discuss and implement the problems. Hence this is one of the Best Data structures And Algorithms Training In Bangalore or Data Structures and Algorithms Training In Hyderabad

Course Details:

Duration: 50+ hrs

time : 7.30 pm

Mode :  Online

Course Fee: 400 usd

Demo:

Demo video1:   Delete a node in BST
Demo video2:   Delete first node in CLL

Trainer Details:

Trainer Details:

Trainer Name          : Mr. Srihari
Qualification            : M.Tech(CSE), IIT Roorkee
Experience              : Software professional with 20 yrs experience in Data structures/C/C++/JAVA/Python/PERL/UNIX/MPI(parallel programming).
Hacker Rank profile: click here

DSA Alumni

Mr Srihari trained nearly 26 students on Data Structures and Algorithms….. He trained ppl from B.tech student to 20 years of real time experienced ppl and students  from various cities in India and Countries like USA, Australia, UK   …etc. click here for Data Structures and Algorithms old batches details

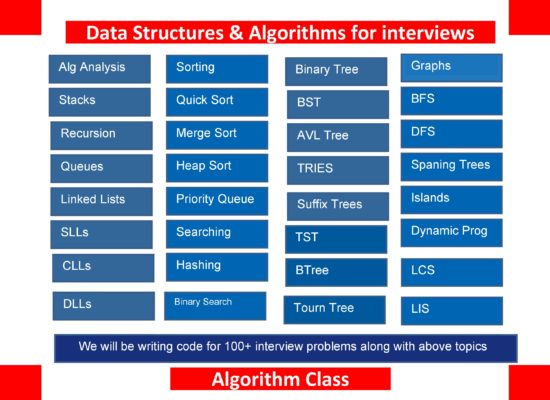
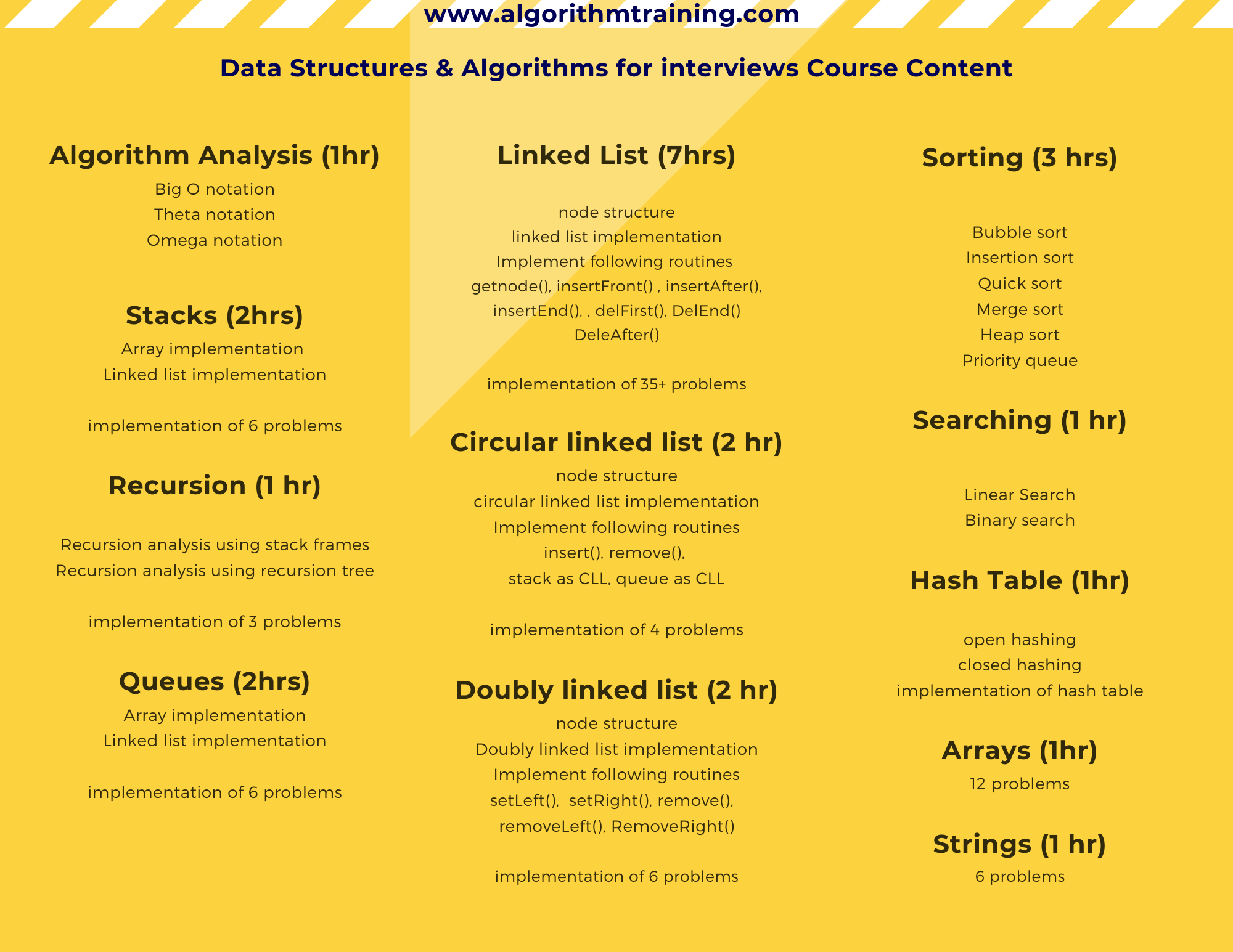
Course Content

Download course content here: Data Structures and Algorithms for Interviews (2272 downloads )

SNO Topic Sub topic Sample questions No. of hrs
1 Algorithm Analysis How to analyse a program

Big O notation

Theta notation

Omega notation

 1
2 Stacks a)Array implementation

b) Linked list implementation

create stack()

isempty()

push()

pop()

 

  

1.Check for balanced parentheses in an expression

2, Manage 2 stacks in an array

3. Check String is palindrome or not

4. Reverse a string

5.infix to post fix conversion

6. evaluate postfix expression

 3
3 Recursion Recursion analysis using stack frames

Recursion analysis using recursion tree

 Analysis of factorial problem

Analysis of fib series

String permutations

Towers of Hanoi

 1
4 queues a)Array and linked list implementation of a queue

create queue()

isempty()

insert()

remove()

b) circular queue

c) double ended queue

 1. Queue using 2 stacks

2. Sort queue

3. Reverse Queue ...etc

 1
5 Linked Lists Why linked list

linked list implementation

node structure

Implement following routines

getnode()

insertFront()

insertAfter()

insertEnd()

DelFirst()

DelEnd()

DeleAfter()

 35 + problems on LL

Implementation of the following problems
 1.Insert new node at front end of linked list
      2. Delete the first node at the front of the LL
      3.Implement Stack using LL
 4. Insert at end of the linked list
5. Insert an element into sorted LL
      6.Insert new node after the given node
      7. Delete the node with data x in LL
      8.Insert the new node after the given node
      9.Find Kth node from head in LL
     10.Find Kth node from back
     11. Swap kth node from front with kth node from back
     12.Find Middle element
     13.Find whether th ll is even length or odd length
     14.Reverse LL
     15. Print LL
     16.find length of ll
17. the Find common node in common to both the lists. 18. delete a node p given in a linked list efficiently
19 Delete kth element from last
20.Insert After Kth Node from last
21. Alternating split of a given Singly Linked List
22 check whether linked list polindrome or not
23 pair wise swap
24 delete N nodes after M nodes
25 Delete alternate nodes of a Linked List
26 Compare two LLs
27. Merge 2 sorted LLs
28. Remove duplicates in LLs
29. add two numbers stored in two LLs
30.Detect loop in LLs
 8
 6 Circular linked list insert()

remove()

stack as CLL

queue as CLL

 1.Implement  stack using circular queue

2.implement circular queue using linked list

3.Split CLL into two halfs

4.Merge 2 CLLs into One CLL

 1
 7 Doubly linked list setLeft()

setRight()

remove()

removeLeft()

RemoveRight()

 DLL NODE structure

1.Implement insert front DLL

2.Implement delete front node

3.Delete Given Node

4.Insert After the given node

5.Insert before the given node

6.Reverse DLL

 

 

 1
8 Binary Tree   and Binary Search trees a) Tree terminology

b) General tree

a) expression tree

b)Binary Tree

e) Tree traversal

PreTraversal()

postTraversal()

inorderTrav()

f) Construct original tree from given pre order and in order traversals.
g) Construct original tree from given post order and in order traversals.

a) createtree()

b) setleft()

c) setRight()

d) createTree()

e) disposeTree()

f) FindKey)_

g) findMin()

h) findMax()

i) find inorder successor, predecessor
j) Tree delete operation
 35 + problems on trees

1.create tree non recursively

2. implement insert a new node into tree

3. implement find min in BST

4.implement find max in BST

5.Implement to delete all nodes in BST

6.Find the given key in BST

7.Find min node in BST

8. Find max in BST

9. Implement preorder traversal

10. Implement inorder traversal

11. Implement preorder traversal

12 implement Delete a node BST

13.Find min in BT
14.find max in BT
15.Program to find  no of full nodes
16.Program to find  no of single nodes
17.Program to find  no of  leaf nodes
18.Find if there exists a path with length K to leaf
19. Find if there exists a path with length K to given node
20.Print path sum at each node
21.Find level of the tree
22. Find level of given node
23.Find least common ancestor of p and q nodes in BT
24 Find mirror copy of the tree
25.Find Given nodes are Siblings or not
26. Find the given nodes are cosine or not
27Find both trees are identical or not
28.Remove all nodes in the given range in BST
29.Print right view of the tree
30.Find the depth of the tree
31.Find Height of the tree
32.Find inorder successor of the node
33.Find diameter of the tree
34.Sorted DLLIST to BST
35.BST to DLL
36.level order traversal of BT
37. Print in spiral order
38. Given BT Is BST or not
39.Reverse Level Order
 10
 9 AVL tree
Rotations
a) LR
b) RL
c) LL
d) RR
 1
 10  Sorting  Bubble sort

Insertion sort

Quick sort

Merge sort

Heap sort

Priority queue

 3
 11 Array 1. given a binary digits like001101 arrange the numbers such that zeroes should follow 1sike 0001111.

2. Find Triplets of a+b+c=k in an array
3. Next Greater element in an array
4.Lead element in an array
5. Arrange RGB in an array
6.Find unique nos in an array
7.Check 2 arrays are equal or not
8.K largest elements in an array
9.find x and y in an array whose sum is K
'10.Merge two sorted arrays without extra space
11. Find missing number
12. Find missing 2 numbers
 2
12 Strings
  1. Find common prefix
  2. Reverse a String
  3. String Permutations
  4. longest common sub sequence
  5. Longest increasing sub sequence
  6. Find a word in dictionary
12 searching Linear Search

Binary search
  1. Sorted array with duplicates write a function that returns the lowest index of an element x in that array
  2. ... etc
2 problems on tries
 1
13 Hashing open hashing

closed hashing
implementation of hash table
 1
14 Tries introduction

node structure

insert

search
2 problems on TRIES
 2
15 Suffix Trees
1
16 Ternary Search Tree introduction

node structure

insert

search

 1
17  B tree introduction

node structure

insert (algorithm)

search (algorithm)

 1
18 Tournament Tree 1
19 Divide and conquer
Merge Sort
Quick Sort
Binary Search
 1
20 Graphs
Adjacency matrix
Adjacency list
BFS
DFS
Spanning tree
Detect Cycle in a graph
Topological sorting
check the given graph is tree or not
Find the number of islands
Find Black Shapes in a Graph
Possibility of finishing all courses with given prerequisites
Clone an Undirected Graph
Knight movement on a chess board
Longest path in an undirected tree
.. etc
 6
21 Greedy Method
Kruskals spanning tre
Primes spanning tree
Disjaskra shortest path
Knapsack problem
Min cost path Matrix
Coin change problem
Longest common sub sequence
Huffman Coding
4
22 Backtracking
print permutations of a String
rat in amaze problem
1
21 Dynamic Programming
Introduction to dynamic programming
memorization (top down)
tabulation (Bottom up)
optimal sub structure
rec solDP solution of
1 Longest common sub sequence
2 Min cost path Matrix
3 Knapsack problem
4 Coin change problem
5 factorial of a numer
6 fibanacci series
7. pattern matching
8.rod cutting
 5